Kuratowski’s 14 set Theorem

Mar 11

‘‘Working problems is a crucial part of learning mathematics. No one can learn topology merely by poring over the definitions, theorems, and examples that are worked out in the text. One must work part of it out for oneself. To provide that opportunity is the purpose of the exercises.’’

James R. Munkres

1. Executive Summary: The Kuratowski 14-Set Theorem

The Kuratowski closure-complement theorem, sometimes referred to as the Kuratowski 14-set theorem, stands as a fundamental result in point-set topology. The theorem asserts that for any subset of a topological space, at most 14 distinct sets can be formed by repeatedly applying the operations of topological closure and set complementation in any arbitrary sequence. First published by Kazimierz Kuratowski in his 1922 dissertation, this result has since gained prominence through its inclusion as a challenging exercise in foundational general topology textbooks (see [4],[5],[6]). The theorem's enduring appeal lies not only in the surprising nature of the number 14 but also in the elegant, non-topological proof that underpins it.

The primary insight of the proof is that the number 14 emerges from the algebraic properties of the operators themselves, rather than from a complex point-set argument. The closure and complement operations generate a monoid whose size is constrained by a specific set of reduction identities. These identities, which simplify any arbitrarily long sequence of operations into a finite number of unique "words," limit the number of distinct sets to a maximum of 14.

Achieving this maximum requires a starting set with a specific "pathological" structure, one that is neither open nor closed and possesses a complex relationship between its interior, closure, and boundary. Simpler sets, such as those that are open, closed, or belong to spaces with trivial topologies, produce a far smaller number of sets. This report will provide a comprehensive proof based on the monoid generated by the operators and will illustrate the result with concrete examples, including two canonical 14-sets and three additional cases that demonstrate why the maximum is not always achieved.

2. Clarification of Nomenclature

The name "Kuratowski's theorem" can be a source of confusion, as it refers to two distinct results from different fields of mathematics. One, which is the subject of this report, is the closure-complement theorem in point-set topology. The other, arguably more famous, is a result in graph theory that provides a forbidden graph characterization of planar graphs. The graph theory theorem states that a finite graph is planar if and only if it does not contain a subgraph that is a subdivision of the complete graph on five vertices $( K5)$ or the complete bipartite graph on six vertices $(K3,3)$. This distinction is crucial for proper understanding, as the two theorems are entirely unrelated in their subject matter, despite sharing a name. This report focuses exclusively on the point-set topological result.

3. Essential Topological Prerequisites

To understand the proof, a working knowledge of basic topological concepts is necessary. A topological space is an ordered pair $(X,\tau)$, where $X$ is a set and $\tau$ is a collection of subsets of $X$ called open sets. These open sets must satisfy three axioms: the empty set ∅ and the set $X$ itself must be in $\tau$; any arbitrary union of open sets must be in $\tau$; and any finite intersection of open sets must be in $\tau$.

4. Properties of the Operators

The proof of the theorem relies on a few fundamental properties of the closure and complement operators that are valid for any topological space.

The closure operator $k(A)$ has the following four properties, often referred to as the Kuratowski closure axioms :

Closure of the empty set: $k(\emptyset)=\emptyset$.
Expansiveness: $A\subset k(A)$. The closure of a set contains the set itself.
Idempotency: $k(k(A))=k(A)$. Applying the closure operation twice is the same as applying it once.
Additivity: $k(A\cup B)=k(A)\cup k(B)$. The closure of a union is the union of the closures.

The complement operator $c(A)$ has one key property that is essential to the proof:

Involution: $c(c(A))=A$. Applying the complement operation twice returns the original set.

A third operator, the interior of a set $A$, denoted $i(A)$, is defined as the union of all open sets contained in $A$. It is the largest open set contained within $A$ and can be expressed in terms of the closure and complement operators as $i(A)=c(k(c(A)))$. Like the closure, the interior operator is also idempotent:

5. The Algebraic Proof of the Upper Bound :The Monoid of Operations

The proof of the Kuratowski 14-set theorem is fundamentally algebraic. The two operators, closure (k) and complement (c), can be viewed as elements of a formal alphabet. The application of these operators in sequence forms a "word" in a formal language. The set of all possible compositions of these operators forms a monoid, a set with an associative binary operation and an identity element. The number of distinct sets that can be generated from a starting set A corresponds to the number of unique "words" in this monoid.

The surprising upper bound of 14 is not a mere coincidence but a direct consequence of the algebraic structure of these operators. The monoid is not infinite because any long sequence of operators can be simplified using a set of reduction identities. These identities provide a finite set of canonical forms for any possible sequence of operations.

6. The Key Reduction Identities

The three primary identities that limit the size of the monoid are derived from the properties outlined in Section 2.3:

Involution of Complement: $c^2=I$. This means that any instance of cc in a sequence of operations can be eliminated, as it is equivalent to the identity operation. For example,
$kcckc$ reduces to $kkc$ which then reduces to $kc$.
Idempotency of Closure: $k^2=k$. Any instance of $kk$ in a sequence can be replaced with a single $k$. For example, $ckckk$ becomes $ckck$.
The Interior-Closure Identity: The most critical identity is $kckc=kckckc$. This identity, which relies on the definition of the interior operator $i=ckc$, effectively prevents the sequence of alternating operations from generating an infinite number of sets. The sequence of alternating $k$ and $c$ operations, which would otherwise continue indefinitely, collapses at a certain point. This property is also related to the fact that $i(A)$ and $c(k(A))$ are idempotent, which can be expressed as $i^2=i$ and $(kc)2=kc$. The existence of these reduction rules ensures that the monoid of operators is finite and its size is, at most, 14.

Note.

The identity $i=ckc$ is equivalent to both $ci=kc$ and $ic=ck$. These can be proved easily using deinitions (see [5] Lemma 1).
It follows that in any $ck$ the $c$ can be moved to right using $ic=ck$.
The maximum number 14 will not change even if we apply $i$.

7. Enumerating the 14 Sets

Starting with an arbitrary set $A$, we can systematically apply the operators to enumerate all possible unique sets. The application of the complement operator on any set $S$ yields $c(S)$, and applying the closure operator yields $k(S)$. Because of the involution property of the complement, any path of operations will be a sequence of alternating $k$ and $c$ operators, with no repeated $cc$ or $kk$ substrings. The maximum number of sets is reached when none of the intermediate sets are equal to any previously generated set.

The enumeration can be organized into two branches: one starting with $A$ and the other with its complement $c(A)$.

Table 1: The Kuratowski Monoid of 14 Sets

Observations

In column 1 the next member (15.) will be $k(c(k(c(k(c(k(A)))))))=k(c(k(c(k(A)))))$ which is the 6th (11.) Similarly, in second column the next member (16.) will be $k(c(k(c(k(c(k(c(A))))))))=k(c(k(c(k(c(A))))))=k(c(k(c(A))))$ which is the 4th (8.).
This proves there are a maximum of 14. The maximum number will be reached when all seven sets in each column are distinct.
There are 6 sets with outer most $k$. These are therefore closed and are 3,4,7,8,12.
Sets with outermost $ck$ are all open and are 5, 6, 9, 10, 13.
In the case of R the only sets which are both open and closed are $\emptyset$ and R. So, if $A$ is different from these two the two sequence of 6 sets in (3) and (4) are different. At most commonality will be only within the group of 6.

The existence of a set for which all 14 of these sets are distinct is what proves the maximum is exactly 14, not merely an upper bound.

8. The Examples: Illustrating the Maximum and Beyond

The maximum of 14 sets is not universally achieved. The actual number of distinct sets generated by the closure and complement operations is highly dependent on the starting set and the underlying topology. For a set to generate 14 distinct subsets, it must be neither open nor closed, and its interior, closure, and boundary must be complex and non-trivial. Such sets are often described as "pathological" in their topological properties. The following examples illustrate this dependency, providing two examples that achieve the maximum and three cases that do not.

8.1 The Canonical Example on the Real Line

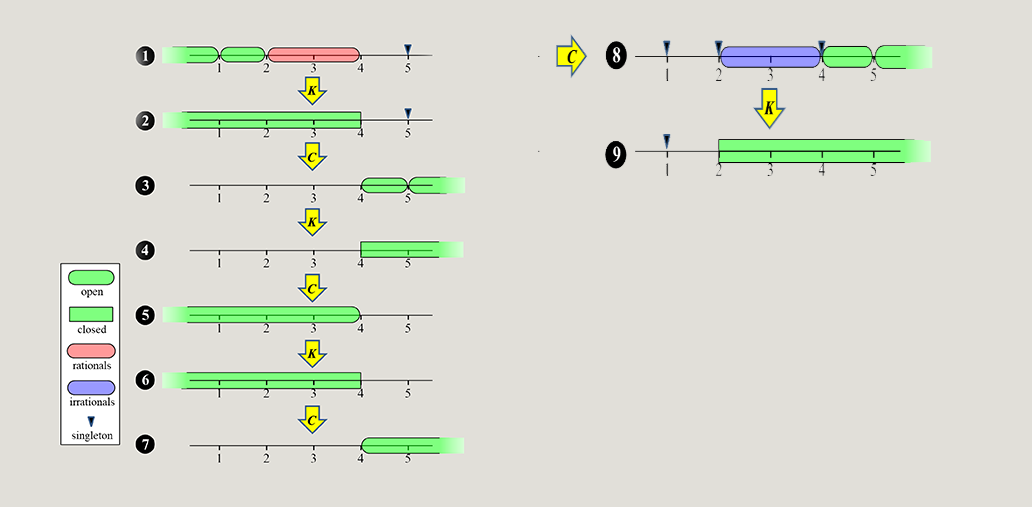
The most common example of a set that generates 14 distinct sets is a subset of the real number line R with the usual Euclidean topology. Consider the set A defined as: $A=(-\infty,1)\cup(1,2)∪((\textbf{Q}\cap (2,4))\cup\{5\}$ .

This set is specifically constructed to contain open intervals, an isolated point, and a dense subset (viz ., rationals) of an interval. The following table provides a step-by-step derivation of all 14 sets. After the first 8 sets, set 9 and a further five sets on the right are precisely the reflections of sets 2, 3, . . . , 7 about the point 3.

Another 14 set

$1.\ A=(0,1)\cup(1,2)\cup\{3\}\cup([4,5]\cap\textbf{Q})$

$2.\ kA=[0,2]\cup\{3\}\cup[4,5]$

$3.\ cA=(−\infty,0]\cup\{1\}\cup[2,3)\cup(3,4)\cup([4,5]\cap\textbf{R}\setminus\textbf{Q}))\cup(5,\infty)$

$4.\ kcA=(−\infty,0]\cup\{1\}\cup[2,\infty)$

$5.\ ckA=(−\infty,0)\cup(2,3)\cup(3,4)\cup(5,\infty)$

$6.\ kckA=(−\infty,0]\cup[2,4]\cup[5,\infty)$

$7.\ ckcA=(0,1)\cup(1,2)$

$8.\ kckcA=[0,2]$

$9.\ ckckA=(0,2)\cup(4,5)$

$10.\ kckckA=[0,2]\cup[4,5]$

$11.\ ckckcA=(−\infty,0)\cup(2,\infty)$

$12.\ kckckcA=(−\infty,0]\cup[2,\infty)$

$13.\ ckckckA=(−\infty,0)\cup(2,4)\cup(5,\infty)$

$14.\ ckckckcA=(0,2)$

8.2 A Distinct 14-Set on the Real Line

Another example of a 14-set on the real line is the set:

$A=\{1/n\mid n \in \textbf{N}\}\cup (3,4)\cup \{4,5\}\cup[6,7]\cup(7,8)\cap\textbf{Q}$.

This set is also designed to have a complex structure. The sequence $\{1/n\}$ has a single accumulation point at 0, which is outside the set. It also contains open and closed intervals and a dense set of rationals within another interval. The existence of multiple examples demonstrates that the phenomenon is not specific to the canonical case but rather is a consequence of the underlying topological complexity of the starting set.

8.3 A Case with Fewer than 14 Sets (Closed Interval)

Consider a simple set like a closed interval $A=[a,b]$ in the standard Euclidean topology on R. The number of sets generated is far less than 14.

$A=[a,b]$.
$k(A)=A$ because $A$ is a closed set.
$c(A)=(−\infty ,a)\cup(b,\infty)$.
$k(c(A))=(−\infty,a]\cup[b,\infty)$.
$c(k(c(A)))=(a,b)$.
$k(c(k(c(A))))=[a,b]=A$.

The operations then repeat, generating a total of only 4 distinct sets. This demonstrates that the simplicity of the initial set's topological properties—in this case, being a closed set—causes a rapid collapse in the number of generated sets. The maximum of 14 is a potential, not a guaranteed outcome.

8.4 The Impact of Topology (Discrete Topology)

The number of sets is also dependent on the choice of topology. Consider any set $X$ with the discrete topology, where every subset of $X$ is defined as an open set. In this topology, every subset is also a closed set because its complement is also an open set.

For any set $A\subseteq X$:

$A$.
$k(A)=A$ because $A$ is closed.
$c(A)=X\setminus A$.
$k(c(A))=c(A)$ because $c(A)$ is also closed.
$c(k(c(A)))=c(c(A))=A$.

The entire sequence of operations generates only two distinct sets: $A$ and its complement. This serves as a powerful illustration that the topological space itself is a fundamental causal constraint. The properties of the closure and complement operators are not inherent to the sets but are defined by the structure of the topological space in which they reside.

8.5 A Non-Trivial Intermediate Case

For a final example, consider the set $A=(0,1)\cup\{2\}$ in the standard Euclidean topology on R. This set is a combination of an open interval and an isolated point.

$A=(0,1)\cup\{2\}$.
$k(A)=[0,1]\cup\{2\}$.
$c(A)=(−\infty,0]\cup[1,2)\cup(2,\infty)$.
$k(c(A))=(−\infty,0]\cup[1,2]\cup[2,\infty)=(−\infty,0]∪[1,\infty)$.
$c(k(A))=(−\infty,0)\cup(1,2)\cup(2,\infty)$.
$k(c(k(A))) = (-\infty,0] \cup[1,2] \cup [2,\infty) = (-\infty,0] \cup[1,\infty]$. This is the same set in 4.

This generalizability has led to a rich field of related problems and research, with modern investigations exploring generalizations that include additional Boolean operations such as union and intersection. While the number of distinct sets can increase or even become infinite when new operations are added, the Kuratowski problem remains a celebrated and foundational result that beautifully connects different mathematical domains.

References

What is Kuratowski's 14 set theorem? Introduction 1 Background knowledge, https://math.osu.edu/sites/math.osu.edu/files/Kuratowski14Sets.pdf
A Note on Kuratowski's Theorem and Its Related Topics https://www.scirp.org/journal/paperinformation?paperid=78128
Kuratowski's 14-Set Theorem, https://www.theoremoftheday.org/Topology/Kuratowski14/TotDKuratowski14.pdf
Steen, L.A. and Seebach, A.J. (1970) Counter Examples in Topology. Holt, Rinehart and Winston, Austin.
Munkres, J. (2017). Topology Pearson.
Kelley, John L, General Topology. Van Nostrand, 1955.
James H. Fife, The Kuratowski Closure-Complement Problem, Mathematics Magazine, Vol. 64, No. 3 (Jun., 1991), pp. 180-182

Tara Radhakrishna Nanda