Introduction
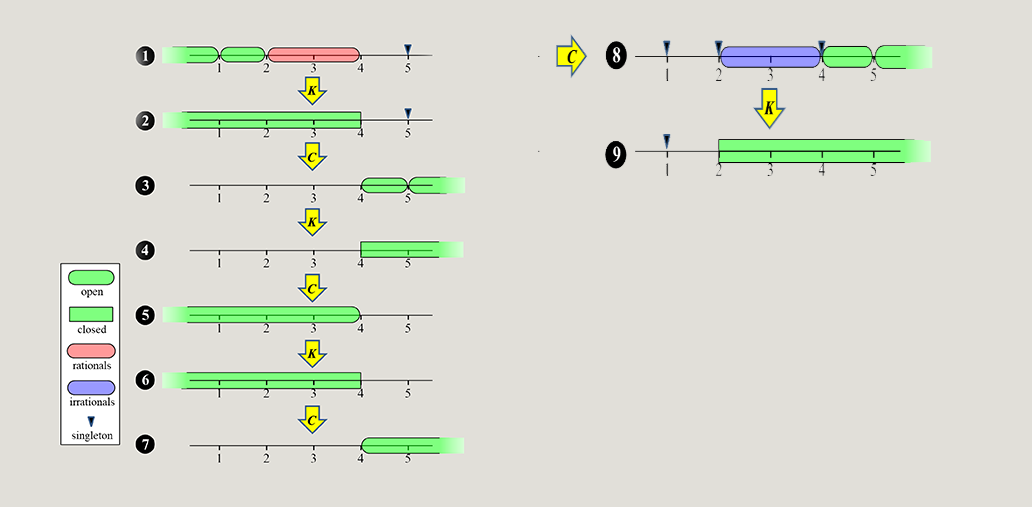
The Kuratowski closure-complement theorem, sometimes referred to as the Kuratowski 14-set theorem, stands as a fundamental result in point-set topology. The theorem asserts that for any subset of a topological space, at most 14 distinct sets can be formed by repeatedly applying the operations of topological closure and set complementation in any arbitrary sequence. First published by Kazimierz Kuratowski in his 1922 dissertation, this result has since gained prominence through its inclusion as a challenging exercise in foundational general topology textbooks (see [4],[5],[6]). The theorem's enduring appeal lies not only in the surprising nature of the number 14 but also in the elegant, non-topological proof that underpins it.
Contents
item 1
item 2
item 3
item 4
item 4